August 25, 2023
4 min read
But Do You Understand The Problem?
George Pólya was a professor of mathematics at Stanford University who taught the likes of John Von Neumann. Pólya spent considerable effort to identify systematic methods of problem-solving. In this post, we will look at one of his most popular problem-solving frameworks.
When presented with any problem, it is very natural to go head-on into problem-solving mode. However, this is not always the most optimal strategy. Here's why:
- You may be solving a problem that has already been solved efficiently.
- You may not be aware of the second order effects and side-effects of your solution.
- You may be solving the wrong problem.
- Your thinking may be subject to cognitive biases.
- ...
By taking a step back and applying Pólya's framework you may greatly improve your thinking and increase the odds of successfully solving your problem.
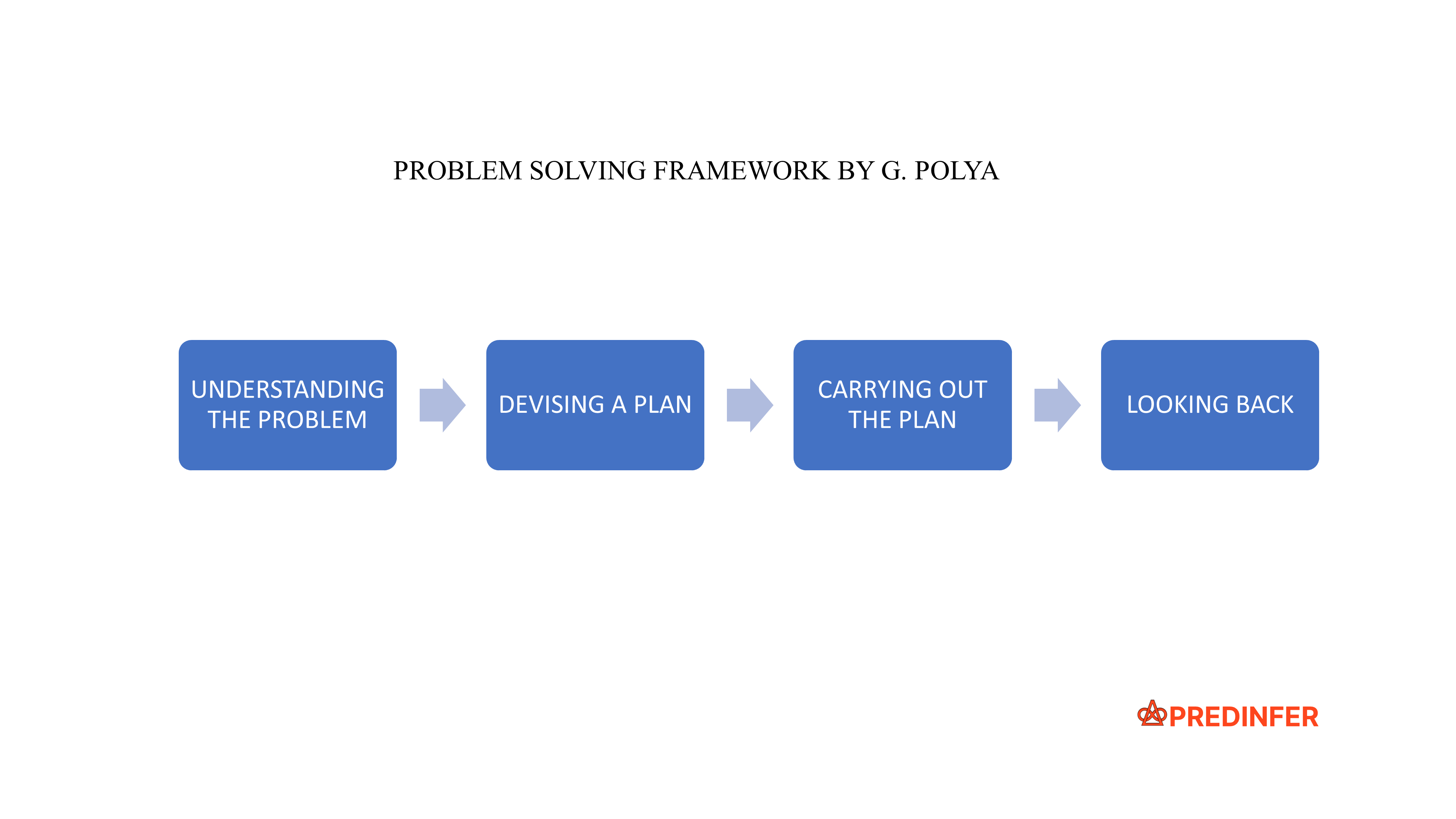
Pólya's problem-solving framework consists of a methodical four-step plan. Before you go through this framework, think of a problem that you are looking to solve right now. Then write down your answers for each of the four steps below.
1. Understanding The Problem
- What is the unknown?
- What are the data?
- What is the condition?
- Is it possible to satisfy the condition?
- Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?
- Draw a figure. Introduce suitable notation.
- Separate various parts of the condition. Can you write them down?
2. Devising A Plan
- Find the connection between the data and the unknown.
- You may be obliged to consider auxiliary problems if an immediate connection cannot be found.
- You should obtain eventually a plan of the solution.
- Have you seen it before? Or have you seen the same problem in a slightly different form?
- Do you know a related problem? Do you know a theorem that could be useful?
- Look at the unknown! And, try to think of a familiar problem having the same or a similar unknown.
- Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?
- Could you restate the problem? Could you restate it still differently? Go back to definitions.
- If you cannot solve the proposed problem try to solve first some related/general/special/analogous problem.
- Could you solve a part of the problem? Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary?
- Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or the data, or both if necessary, so that the new unknown and the new data are nearer to each other?
- Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?
3. Carrying Out The Plan
- Carry out your plan.
- While carrying out your plan of the solution, check each step.
- Can you see clearly that the step is correct? Can you prove that it is correct?
4. Looking Back
- Examine the solution obtained.
- Can you check the result? Can you check the argument?
- Can you derive the result differently? Can you see it at a glance?
- Can you use the result, or the method, for some other problem?
Of course, at first glance the framework may seem abstract. The only way to make it work for you is to methodically apply it to a problem that you care about.
So the next time you are stuck on a problem or simply looking for inspiration, refer back to this framework and apply it to your problem.
"If there is a problem you can't solve, then there is an easier problem you can solve: find it." - George Pólya